Numerical Methods for
Inductance Calculation

Part 2 – Inductance Calculation Refinements

B) Circular Filaments and Helical Corrections

In this section we return to the summation method of inductance calculation, and consider some corrections to account for the fact that the coil is a helix rather than a series of perfectly circular rings. This has several consequences, but we will just consider the following two, for the time being:

• One turn is longer than an equivalent ring;
• The distance between turns is less than the pitch!

We will address these items in the following subsections. However, it will make things easier to follow if we examine the geometry of a coil in greater detail. Consider the following three turn coil:

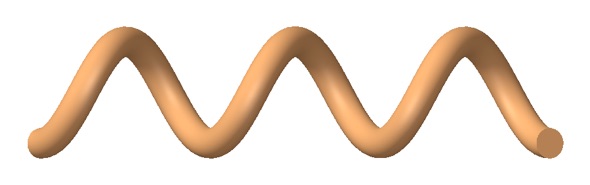
For this example, the pitch has deliberately been made large in order to accentuate the effects of helicity. Let's look at a cross section of the coil taken through the coil axis:

It can be seen that the cut face of the wire is elliptical, because the cut has been taken parallel to the axis, while the wire lies at an oblique angle.

If we take the original coil and cut it open, along the bottom as shown in the diagram at the right, then unroll it (but otherwise keep all the pieces in the same relative positions) and lay it flat, we end up with the conductors arranged as shown in the diagram below:

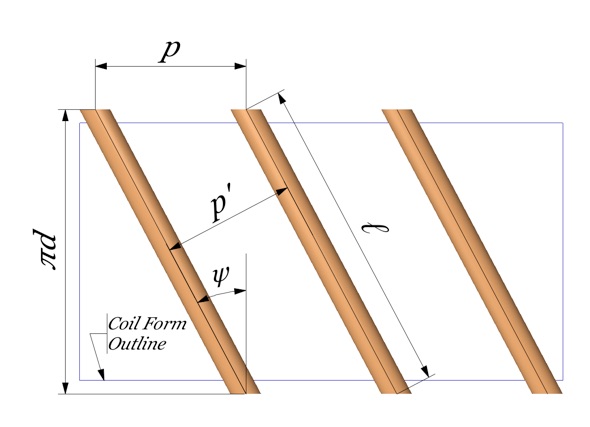
Note that as the coil form is unwrapped, the conductors will stick beyond it by an amount equal to half of the conductor diameter. But by convention we measure diameter to the centre of the conductor. And therefore the circumference is π d.

We see that the pitch p which is measured parallel to the coil axis is not the same as the conductor centre to centre distance p'. In fact, even if the coil were closely wound with the turns tight together, the pitch would still be greater than the wire diameter. Hence, the pitch must always be greater than the wire diameter. This fact is non-intuitive, and if it is overlooked it can result in coil geometry calculations that are incorrect and very confusing.

It can also be seen that the length of one turn ℓ is greater than the coil circumference π d.

We will define ψ (Greek letter psi) as the pitch angle as shown in the diagram. From basic geometry we have the following relationships:

ψ = Arctan(p/π d)

ℓ  = √(p²+(π d)²) = π d/cos ψ

p' = p cos ψ

From the above it can be seen that for a close-wound coil, of wire diameter d_W, the pitch p_c is slightly greater than d_W, and is given by the close-wound pitch angle ψ_c:

ψ_c  = Arcsin(d_W/(π d))

p_c = d_W/cos ψ_c

Turn Length Correction

If the coil consisted of a series of parallel perfectly circular rings, then we would use the standard formula for the circumference of a circle to calculate the length of a turn:

ℓ = π d

However, we have already shown above that the actual turn length for a helix is:

ℓ  = √(p²+(π d)²)

It's therefore logical, that the greater length of turn will have an effect on the mutual inductance calculated by elliptic integral formulae (10), (11) or (12). We can compensate for this by making an adjustment to the value of the loop diameter used in the formulae. We can calculate an adjusted diameter d', so that it gives a correct helical turn length:

d' =  ℓ/π = √(p²+(π d)²)/π

which simplifies to:

d' = √((p/π)²+d ²)

We can therefore use d' in place of d in the Mut() function to provide helical turn length correction.

Turn Spacing Correction

Similarly, we see from the above relationships, that the distance between adjacent turns is not equal to the pitch p, but rather, p' which has already been given as:

p' = p cos ψ

We can therefore use p' in place of p for the distance between turns, at least for turns which are not too far apart. However, this cannot be applied generally. It should be apparent from the diagram, that for turns which are distant from each other, the spacing will approximate the pitch times the number of turns separating the two turns being considered. Therefore, any correction for turn spacing must vary smoothly between cos ψ and 1 as the distance between turns increases.

This is as far as I've progressed on the turns spacing correction, for the following reasons:

• For coils that are closely wound, p' and p are virtually equal, and so no correction is required.
• For coils with considerable space between turns, then the assumption that the turns are circular becomes invalid and it is difficult to justify a simple spacing correction without having some means to test the validity of the correction.

I plan to address this correction in the future once I've developed a means to test it. This will include coding of an independent inductance calculation, which takes helicity into account in order to have a means to cross check the corrections. This work is now partially completed as is discussed in Part 2c.

Continue to: