Multi-Layer Coil Inductance Calculator

Use this calculator to find the inductance of a multi-layer coil.

For single layer coils, you may also use the following simpler calculators:
Solenoid Inductance Calculator
Rectangular Coil Calculator

Refer to the bottom of the page for explanation of input variables and other notes.

Note: This calculator is also suitable for flat spiral (pancake, spiderweb, etc.) coils, by setting the number of turns per layer, N_T to 1 and setting the number of layers N_L to the number of turns in the spiral.

See bottom of this page for detailed information and instructions.

**---Calculator---**

Input Parameters:
Units:
Number of Turns per Layer - N_T:
Number of Layers - N_L:
Diameter of -		mm
Coil Shape: No. of Polygon Sides:
Axial: and Enter:		mm
Radial: and Enter:		mm
Operating Frequency (Optional):		kHz
Conductor Size - d:
Wire Diameter Including Insulation - d_i:		mm	Auto Calculate

Results:
Conductor Diameter:	***
Axial Pitch:	***
Radial Pitch:	***
Coil Length:	***
Coil Outside Diameter:	***
Total Wire Length:	***
Skin depth/wire diameter ratio:	***
Base Inductance L_S:	***	µH
Frequency Correction L_I:	***	µH
Corrected Inductance:	***	µH

Notes:

Revised 2023-01-29

Please scroll to the bottom of the page for a detailed revision history.

Note that as of the 2019-03-03 revision, you now have additional input options for coil length/pitch, winding depth/pitch and coil diameter. Previously, all of these dimensions were measured from centre to centre of the applicable conductors (as shown in the diagram below). This means that the inner diameter would be one wire diameter greater than the coil form diameter. This made it a bit cumbersome for the user. Now, the input options in the popup menus include the actual coil form dimensions and overall dimensions as well as the original centre-centre dimensions. The original centre-centre menu options are now indicated with “C-C” to avoid confusion. The displayed output values for Coil Length and Coil Outside Diameter are now all overall dimensions. An additional diagram will be added at a later date to show the new dimension types.

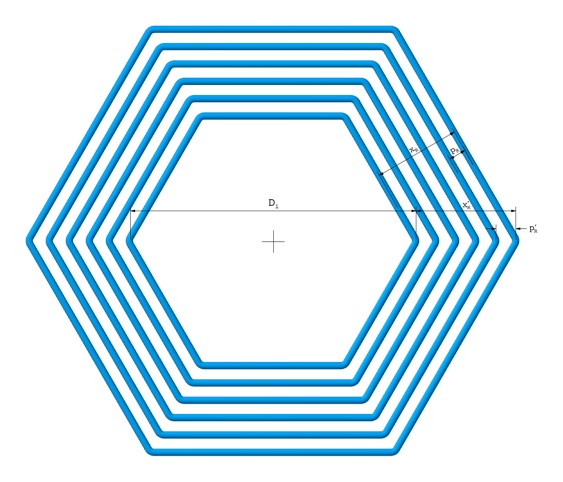
Please refer to the diagram below for terminology.

All length, diameter and pitch measurements are from centre to centre of the conductors as shown.

Definition of Parameters:

ℓ_A - Coil Length C-C^*
x_R - Radial dimension of winding (winding depth) C-C
p_A - Winding pitch along axis C-C
p_R - Radial winding pitch C-C
D_o - Outside Diameter of Coil C-C
D_i - Inside Diameter of Coil C-C
d - Diameter of conductor (excluding insulation)
d_i - Outside diameter of conductor including insulation
N_T - Number of turns per layer (N_T= 6 in the diagram)
N_L - Number of winding layers (N_L= 5 in the diagram)
N_S - Number sides of polygon (for polygonal coils)

Dimension & Variable Notes

* The notation C-C indicates that the dimension is measured from centre to centre of the conductors as shown in the diagram.
Uppercase D parameters refer to overall coil diameters while lowercase d parameters refer to conductor diameters.

General Notes

Calculation Method:
This calculator uses Maxwell’s formula for the mutual inductance between two circular filaments, applied to every combination of wire pairs in the coil, and then summed to determine the total inductance. For polygonal coils, an equivalent circular coil is determined according to a method by F. W. Grover, and the inductance is calculated from the equivalent coil. More information about these calculations is given in Calculation Methods Part 1c.
Wire size:
You may enter conductor size either as diameter in mm or AWG gauge number in the Conductor Size field. Select either ‘AWG’ or ‘mm’ from the popup menu as appropriate. When entering conductor size as AWG, sizes larger than 0 may be entered as 00, 000, etc., or 2/0, 3/0, etc. Although AWG sizes larger than 4/0 do not officially exist, the calculator will accept them and handle them according to the AWG standard ratio between successive sizes of 1.1229322.Insulation diameter d_i is required to be entered only in the case of a close wound coil (see next item). For enamelled magnet wire, you can leave the Auto Calculate box checked, and the calculator will automatically determine the insulation diameter. For other insulation types, uncheck the Auto Calculate box, and enter the actual insulation diameter in the Wire diameter including insulation field.
Close Wound Coils:
For close wound coils, set the axial and radial dimension fields to zero or leave them blank. In Wire diameter including insulation field, enter the value for the insulation diameter, or check the Auto Calculate box as explained above. The calculator will automatically set the correct winding pitch.
Universal/Honeycomb/Basket-weave Coils:
Inductance is essentially independent of the order in which the turns are placed on the coil. As long as it is possible to count the turns per layer and number of layers accurately, then the calculator will determine the correct inductance. In the case of these space wound type coils, it may not be easy to determine the effective number of turns per layer beforehand, making it difficult to predict the final dimensions, and hence, the inductance value. However, coil length ℓ_A is easily determined beforehand, and if a test winding is made, total turns, and number of layers can be easily counted. From this test winding data, the turns per layer can be found by dividing total number of turns by number of layers. This information can then be used to design the final coil.
Frequency Correction:
Optionally, enter the intended operating frequency, and the calculator will calculate a frequency correction due to skin effect. This correction is very small and can be neglected in most cases. Note that no correction is done for proximity effect.
Self-Capacitance Effect:
The effect of self-capacitance causes coil inductance to read lower than its true value, when measured on inexpensive inductance meters. Because multi-layer coils tend to have much higher self-capacitance than single layer coils, the difference between measured and true inductance can be expected to be greater. Therefore, one should be cautious when interpreting the measurements from inductance meters if they appear lower than expected.
Coil Form Shape:
The coil form may be either circular or polygonal. For polygonal coils, select Polygonal from the Coil form popup menu, and then in the Number of Polygon Sides input field, enter the number of sides. For circular coils, leave the popup menu set to Circular, and leave the Number of Polygon Sides input field blank.
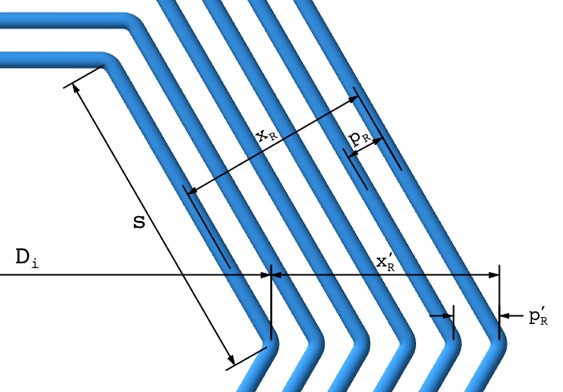
Polygon Measurements (see diagrams below):
Inner diameter D_i is the same as the diameter of the circumscribed circle of the inner polygon. It is measured, in the case of a polygon with an even number of sides, from one inner vertex across to the opposite inner vertex. For a polygon with an odd number of sides, the measurement is taken from the centre axis to an inner vertex, and that value is then doubled. Alternatively, measure the length, s, of a side, and then the diameter is given by:

D_i = s/sin(π/N_S)         (Angle in radians)

   or

D_i = s/sin(180/N_S)     (Angle in degrees)

Note that the true radial pitch p_R is less than the radial distance between vertices p_R', by a factor of cos(π/N_S). Likewise, the radial depth of winding, x_R, is smaller than x_R', the distance between the innermost and outermost vertex by the same factor. However, since it is generally easier to measure along the vertices, the calculator is designed to accept the p_R' and x_R' values as measured along the vertices. Therefore: Do not use the p_R and x_R values for polygonal coils.

Polygonal Coil

Viewed along axis:

Dimension detail:

Back to:
Calculators
Radio Theory
Home
This page last updated: January 28, 2023
Copyright 2010, 2023 Robert Weaver

Revision History

2023-01-29

This page has been completely rebuilt and uploaded in conjunction with a major update of the site to replace the original web development software.
The calculator portion of this page is no longer embedded in an iframe, which should finally fix some known issues with the bottom part of the calculator being cut off in some browsers.

2019-03-03

The 2017-11-30 revision did not correctly address some of the displayed calculated dimensions. There were also several calculation errors caused by incorrectly calculating length as NT × P (Number of Turns × Pitch) when it should have been (NT – 1) × P. Similarly, coil depth calculations were incorrect due to using NL instead of NL–1, where NL is number of layers. The result of these, in most cases, was simply the incorrect display of the coil length and diameter. However, in certain instances, it could also have resulted in an error in the calculated inductance, depending on the selected input popup menu options. The amount of error would vary from negligible for large NL and NT (greater than 20), to fairly significant for small NL and NT (less than 5). Many thanks to the people who noticed the error and reported it: Richard, Brad, Sam and Walt.
Added additional input options for entering coil length and diameter.

2017-11-30

Minor calculation changes to address errors in the displayed coil dimensions.

2015-08-24

Entire site rebuilt and uploaded using updated web publishing software. This should address the issue of the bottom part of the calculators being cut off on some web browsers, which made some display fields invisible.

2014-01-28

Original version uploaded.