Numerical Methods for
Inductance Calculation

Part 1 – Elliptic Integrals

C) Multi-Layer Coils

Until now, we have dealt with single layer solenoid coils. However, Maxwell's elliptic integral formula [11a] for circular loops can be applied just as easily to coils consisting of multiple layers of windings. It's just a matter of calculating the mutual inductance between every pair of turns and taking the sum. However, while this may be easy to code it can result in a program which takes a very long time to run. For a coil with N turns, there are N² pairs of turns. As long as N is not too large, this won't matter much. However, as N gets larger, the program will get slower and slower, eventually becoming too slow to be practical. In this section we will look at ways of improving performance.

The naïve approach to code a program to calculate the mutual inductance between all pairs of turns in a coil is to use two nested loops as in the following pseudo-program:

Now, since the mutual inductance between turn i and turn j will be the same value as the mutual inductance between turn j and turn i, it's only necessary to calculate one of these values and then multiply by two. This is done very easily by changing the limits of the loops, as follows:

This reduces the number of iterations to slightly less than half the number of iterations from the previous example. The exact number of iterations in the second example is equal to (N²−N)/2. In the last program line, the value of the sum of mutual inductances M, is doubled to account for the reduced number of iterations. There is another difference between the two programs. The second program will never calculate the mutual inductance between one turn and itself, because i will never be equal to j. We still need to calculate this value, but it is calculated differently from the others as was discussed Part 1B. When using the first program, it is necessary to add an if then...else construct to check for this condition and then handle it differently. Having to add this extra condition test in the inner loop will further decrease performance. Using the second technique, additional code still needs to be added to sum the self inductance of each turn, but the number of additional iterations is simply N. The modified pseudo program is shown below:

The total number of iterations is now (N²+N)/2, which is still significantly smaller than in the first example. By comparison, for the single layer solenoid which was treated in the previous section, we were able to reduce the number of iterations to just N. For a multi-layer coil, the (N²+N)/2 iteration count is the worst case; there are certain special cases where we can do much better. However, we will begin with a general case based on the last example, and address the special cases later.

General Case Multi-Layer Coil

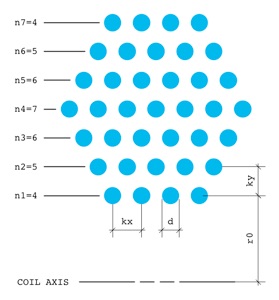The general case is for a multi-layer coil with an arbitrary number of turns on each layer; i.e., each layer may have a different number of turns. This diagram shows an example cross section of a seven layer winding where the innermost layer has four turns, with each successive layer increasing by one turn up until layer 4, and then decreasing by one turn thereafter, giving a hexagonal cross section. Wire diameter is d. The radius of the innermost layer is r₀. Spacing between layers (radial pitch) is ky. Spacing between turns on each layer (axial pitch) is kx. It is assumed that each layer is centred over the previous layer. This is a reasonable approximation for a coil where the winding cross section is approximately circular.

The Open Office BASIC code is as follows:

The program allows for up to ten layers of windings. It can be easily modified to accommodate more layers. Each layer may have a different number of turns. It is assumed that each layer is centred over the previous layer, and the turns on every layer will have the same pitch kx. The centre to centre spacing between layers is ky for all layers.

The shortcomings of Open Office BASIC make for somewhat clunky programming. Several lines are devoted to loading an array with the n1..n10 (turns per layer) arguments. Variable n1 is the number of turns on the innermost layer, and n10 the turns on the outermost layer.

The method of keeping track of layers could be approached a number of ways. A for..next loop to count layers could be used. However, it was decided that it would be simpler overall just to count turns and then determine the applicable layer from the absolute turn number. To make this simpler, the array Nturns() is converted from turns per layer to a running total of turns on the current layer plus total of turns on all previous layers. Then the variables iLayer and jLayer (for turns i and j respectively) are easily calculated.

Variables ix, iy, jx and jy, are the axial position and radius of turn i and turn j respectively.

The mutual inductance between turns is calculated using function Mut() which was described in Part 1B.

This program could be made even more general by adding more arguments to allow the user to specify a different axial offset, radial offset and pitch for each layer individually. However, the program as it is, should be general enough for most situations.

Execution speed, while not spectacular, is not too bad as long as the total number of turns is not too great (i.e., 100 or fewer). This is the cost of trying to keep things general. Performance can be improved considerably for certain special cases. For example, as discussed in Part 1B, the N² iterations was reduced to N iterations in the special case of the single layer solenoid.

Multi-Layer Coil With Rectangular Winding Cross Section

For the next case we will consider a multi-layer coil where each layer has the same number of turns. Hence, the cross section of the winding is rectangular as shown in this next diagram. 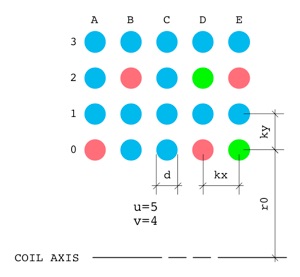In this case, the variables d, kx, ky and r0 have the same meaning as before. The variables n1..n10 are replaced by u and v. The number of turns per layer is now constant and is designated by variable u. The number of layers is designated by variable v. For the purpose of the following discussion, each layer will be designated by a number (starting at 0), and each turn in the layer will be designated by a letter, as indicated by the numbers and letters at the left and top of the diagram. Hence the innermost layer is 0 and the outermost layer is 3. The lower left turn is A0 and the upper right turn is E3.

Now, let's consider the pair of turns A0-B2 shown in red, and also the pair D0-E2 also shown in red. It is readily apparent that the mutual inductance for pair A0-B2 will be the same as the mutual inductance for pair D0-E2, because their respective radii are identical and their respective axial spacings are also identical.

Before we go any further, let's define a convention for specifying pair configurations that are equivalent for calculating mutual inductance. Since horizontal (axial) spacing will always be multiples of kx, let us define the first parameter nx as the number of multiples of kx for this spacing. And since the radial spacing will always be a multiple of ky, then we can define a second parameter ny as the number of multiples of ky for the radial spacing. We will write the configuration in the format: {nx,ny}. Hence, for pair A0-B2, the axial spacing is 1×kx and the radial spacing is 2×ky, so we would write the configuration as {1,2}. Pair D0-E2 also has configuration {1,2}. For the purpose of calculation of mutual inductance, it makes no difference whether the values are positive or negative. The mutual inductance is the same. So, all values used in the configuration specification will be absolute values. Consequently, the pair D2-E0 shown is green, which is a mirror image of pairs A0-B2 and D0-E2, has the same configuration {1,2}.

We soon run into a problem though. According to this definition, pair A1-B3 would also have a configuration {1,2}, but since the radii of A1-B3 are different than those of A0-B2 it won't have the same mutual inductance. We need to add an additional parameter. We will define parameter y as the row number on which the innermost turn of pair is situated. The new format will be {nx,ny,y}. Therefore pairs A0-B2, D0-E2, and D2-E0 will all have a configuration of {1,2,0} and pair A1-B3 will have a configuration of {1,2,1}.

We can see that there are eight pairs which have configuration {1,2,0}, eight pairs which have configuration {1,2,1}, and we can continue onwards and upwards to count all of the pairs for every possible configuration. Having done this, we only need to calculate the inductance value once for each configuration, and then multiply it by the number of times the configuration occurs. One would hope that there is a systematic way of specifying all of the configuration patterns and of figuring out how many there are of each. With a little perseverance and much coffee consumption, a pattern does emerge. For a coil of u turns per layer and v layers, the value ny will range from 0 to v−1. For each of these values of ny, the variable nx will range from 0 to u−1, with the one exception that when ny=0, then nx will range from 1 to u−1 (the zero case is omitted). For each of these combinations of ny and nx, the variable y will range from 0 to v-ny−1. Naturally, three nested program loops will be used to control the values of nx, ny and y, using the ranges discussed here. This will then loop through each possible configuration exactly once.

Now that we know how to loop through each possible configuration, we also need to know how many times each configuration actually occurs in the coil. Again a bit of manual simulation and analysis reveals a pattern. In general, configuration {nx,ny,y} occurs 4(u−nx) times, except when either nx = 0 or ny = 0 (mirror images disappear in these cases), then the configuration occurs 2(u−nx) times. This also takes into account the fact that every pair must be counted twice (e.g., we need to count both pair A0-B1 as well as B1-A0). Although this has been a bit complicated to figure out, the resulting program turns out to be surprisingly simple. The Open Office BASIC code is as follows:

The Javascript version is as follows:

The number of iterations required to calculate the self inductances is always equal to v, regardless of the number of turns per layer. The number of iterations required to calculate the pair mutual inductances is equal to:

(uv+v²u)/2-v

Hence, the total number of iterations is:

(uv+v²u)/2

When v=1, then the coil is a single layer solenoid, and the number of iterations works out to be simply N which is exactly the same as for Lcoil() in in Part 1B. When u=1, the coil is flat spiral, and the number of iterations works out to be:

(N²+N)/2

which is the same as for the previous function LayeredCoil(). This is the worst case because every turn has a different radius and therefore every pair of turns is a unique configuration. For the remaining cases where u>1 and v>1 the performance falls somewhere between the two extremes. For the case u=v, where the number of turns per layer equals the number of layers, then the number of iterations is:

N(1+√N)/2

So, for multi-layer coils with an approximately square cross section, function RectangleCoil() offers a significant speed advantage over function LayeredCoil(). As an example, for u=v=10, then N=100, and LayeredCoil() would perform 5050 iterations while RectangleCoil() performs only 550 iterations. The trade-off, as it often is, is speed versus flexibility.

Thus, the main virtue of this program, is that it always performs the minimum required number of iterations, regardless of number of layers and turns per layer, thus making it unnecessary to substitute more efficient programs for special cases.

An Online Calculator for Multi-Layer Coils is now available.

Multi-Layer Coils on Polygonal Coil Forms

Closewound multi-layer coils can easily be wound on circular forms, each layer sitting directly on top of the previous layer. However, in cases where it is desired to have space between the layers, some means must be provided to separate them. One option is to place a thick sheet of insulating material between each layer. However, this has at least a couple of disadvantages. This material will reduce the Q-factor of the coil, and will increase the self-capacitance of the coil. Also, for coils in power circuits, spacing may be necessary to allow coolant (air or some liquid) to circulate between the windings, and a thick sheet of insulating material will interfere with this. A common alternative approach is to use a polygonal coil form where the wire is wound on insulating pegs or other guides located at the vertices of the polygon. While this may make winding the coil easier, it introduces additional complications.

One thing which may not be immediately obvious is that the spacing of the winding guides will not be the same as the radial pitch. This is illustrated in the following diagram.

Here, the coil form is a 7-sided polygon and has two layers of windings. We are looking at it in the direction of the axis. Radial spacing guides are separated by a distance of 0.500 (arbitrary units). However, notice that the spacing between conductor 1 and conductor 2 is only 0.450. The reduction factor is equal to the cosine of half of the angle between the spokes of the coil form. Or, more simply, for a polygonal form with the number of sides equal to N_S, the spacing reduction factor is equal to cos(180/N_S), when working in degrees, or cos(π/N_S) when working in radians.

Now, looking at the actual inductance calculation, we refer back to the treatment given at the end of Part 1b regarding polygonal single layer coils. The method given is that of Grover [2], and unfortunately, he doesn't say this method is valid for multi-layer coils. So, our only justification for using this method is that there doesn't appear to be any other method available. At the same time, it's reasonable to expect that it should give better correction than no correction at all.

The numbers of the last section won't be repeated here. Suffice to say, the inner and outer radii of the polygonal form are converted to equivalent radii using the weighted formula of Part 1b, and then the radii of any intermediate layers are interpolated from those values. An equivalent ky value can then be calculated, and then these equivalent values are used in the above RectangleCoil and LayeredCoil functions to calculate the inductance.

There are two degenerate cases of a multi-layer polygonal coil which can be checked. The first is the case of a single layer coil treated in Part 1b using the weighted formula, which already have been verified to an accuracy of within 1% for most coils. The second degenerate case is that of a coil with only one turn per layer, i.e., a spiral coil. Fortunately, there are formulae available [2] (page 176) for flat spirals with polygonal turns. So, these cases can be checked. From comparing numbers with various examples of flat polygonal coils, it appears that the true value of inductance lies between the value calculated using the weighted formula in Part 1b, and the value calculated assuming a round coil enclosing the same area. Therefore, it is suggested that both methods be used to get the maximum and minimum values. A simple average of the two values is likely to be close enough for all practical purposes.

Continue to: