Numerical Methods for
Inductance Calculation

Part 1 – Elliptic Integrals

D) Special Types of Coils

The Mystery Crystal Set Coil

In these discussions of numerical methods for inductance calculation, it's very easy to lose touch with reality. Every so often, it's a good idea to look at a real world application, and compare the theoretical predictions with the actual numbers.

The Mystery Crystal Set, which was first described in the July 3rd, 1932 Brisbane [Australia] Sunday Mail (page 23), is unique in the way that its main coil is wound. Because of the periodic resurgence of the Mystery Set's popularity (and partly because of its 80th anniversary), it may be interesting to have a look at the coil and develop a way of analyzing its parameters. The Mystery Set circuit is reproduced below:

One of the more interesting characteristics of the Mystery Crystal Set is that there is no apparent signal path between the antenna and ground. The antenna is connected to the primary, while the circuit's only ground point is connected to the secondary. This set makes use of the inter-winding capacitance to complete the signal path. By means of a two position switch, the antenna can be connected to either end of the primary winding, giving either a Selective or Broad tuning characteristic. Presumably, the Broad setting also gives more volume. (I've reproduced the schematic as it originally appeared. However, it should be noted, that if the coil primary and secondary leads are located the way the diagram implies, then the Broad-Selective switch positions are likely backwards.)

The Mystery Set is described by Ray Creighton on the Historical Wireless Society Site, and is an interesting read:

http://www.hws.org.au/.../mystery.html

The coil has the primary and secondary wound side by side (i.e., bifilar). In the original design, a 3 inch (75 mm) diameter coil form was used. The primary was close-wound 12 turns. Then, after the 12th primary turn, the winding continued with the primary and secondary close-wound side by side for the next 25 turns. The secondary was then terminated, and the primary then continued on for another close-wound 13 turns. Thus, the primary has a total of 50 turns, and the secondary has 25 turns.

A very thorough analysis of the mystery crystal set has been given previously by Ben Tongue on his webpage:

Mystery Crystal Radio Circuit Analysis

My own findings essentially corroborate those of Ben Tongue, although I've limited my analysis, as much as possible, to just the coil part of the receiver.

The following diagram shows a cross sectional view of a smaller version of the mystery coil, with a 14 turn primary (blue conductors), and a 6 turn secondary (red conductors). The number of primary and secondary turns are designated by nP and nS respectively. The start position of the secondary is designated by the variable a and is equal to 5 in this example.

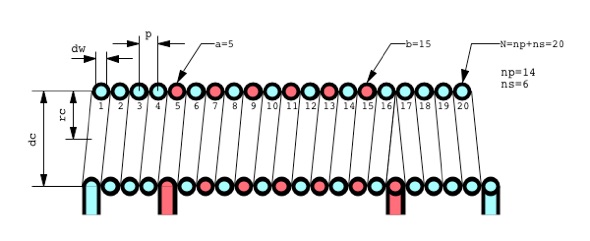
Note that in both the original coil and the one shown in the diagram, the secondary is not exactly centred. In order for the secondary to be centred, the total number of primary and secondary turns would have to be an odd number. Also, it can be a bit confusing when counting turns. As in most cases, it's easier to count turns on the side away from the leads, and that is what we will do here.

From the diagram we can also make note of several important characteristics:

• The primary winding has a variable pitch: initially p, then 2p, and finally p again;
• The secondary winding has a constant pitch of 2p
• If the coil has the primary and secondary connected in series then it effectively becomes a single winding constant pitch coil of pitch p, and total turns N=n_P+n_S turns (20 turns in the diagram example).

(If you're not interested in the derivation of the Mystery coil calculations, and only want to see the results, then go to the Practical Example further down this page.)

In the previous parts of the discussion of inductance calculation, we've demonstrated that it is a simple matter to calculate the inductance of a solenoid with a constant pitch. For this reason it is relatively trivial to calculate the inductance of the secondary winding. Likewise, we can calculate total inductance of the series connected primary + secondary windings.

The formula which relates primary and secondary inductance, to mutual inductance is as follows:

L_T = L_P+L_S+2M

where L_T is the total inductance when primary and secondary are series connected, and M is the mutual inductance between the primary and secondary windings. Since we can easily calculate L_T and L_S using the methods previously described, it can be seen that if we calculate one of the remaining variables, then the other remaining one can then be determined from the above formula.

An efficient method of calculating either L_P or M is not immediately apparent. We can, of course, use a brute force calculation of every combination of pairs of turns. For example, the following Basic program will calculate the self inductance of the primary winding:

The program input parameters are as indicated in the above diagram. The actual calculation of the mutual inductances is done by calling the function Mut() which has been described previously in Part 1b.

In this discussion, the positions of the various turns of the winding will be designated as shown in the diagram just below the upper half of the coil cross section, and numbered from 1 to 20. Hence the primary winding starts at position 1, and the secondary starts at position 5.

It can be seen that the distance between any two turns is equal to the absolute difference between their positions multiplied by the pitch p. At the beginning of the program, the position of each primary turn is calculated and stored in the array Locn(). This makes for simple distance calculation later. The remainder of the program is simply two nested loops which calculate the mutual inductance between every pair of primary turns. This general method has been described in detail in parts 1b and 1c.

Although this program is not highly efficient it provides a means to cross check more efficient algorithms. The importance of this cross check will soon become apparent.

In the case of a single layer coil with constant pitch we have seen that the number of unique spacings between turns is equal to the number of turns N in the coil. Therefore, we only need to call the Mut() function N times, and then multiply each result by the number of occurrences of that spacing. For this type of coil, for a spacing of kp (where k is any integer from 0 to N, and p is the pitch) the number of occurrences is simply N−k. Alas, in the mystery coil, there is no simple formula for the number of occurrences of either the primary turn pairs or the primary-secondary mutual inductance pairs. There is a formula though; it's just not very simple.

As mentioned above, we can calculate either L_S or M and then determine the other quite simply. Probably the lesser of two evils is the calculation of M, and that's how we will proceed. To begin, it's a good idea to work out the pair count manually for the first few spacings and then see if a pattern develops. We will count the number of occurrences of a red (secondary) turn paired with a blue (primary) turn of each possible spacing. It's obvious that there are no mutual inductance pairs with zero spacing. For a spacing of 1, we can see that the red turn at position 5 has a blue neighbour spaced one position away at position 4, and it has a neighbour at position 6 also one position away. Likewise, the red turn at position 7 has two neighbours spaced one position away at positions 6 and 8. So, we see that the number of pairs spaced 1 position apart is equal to 12 in this example. We can see that, in general, the number of pairs spaced one position apart will be equal to 2n_S.

Now let's consider the turns spaced two positions apart. We see that the red turn at position 5 can be paired with a blue turn at position 3. However, when we look at the turn located at position 7 we see that it's not a blue turn; it's a red turn, so we can't count it as a mutual inductance pair. Only pairs of dissimilar colours can be counted. Next, when we look at the red turn at position 7, we've already seen that it can't be paired with turn 5, nor can it be paired with turn 9. The same thing happens with turns 11 and 13. Finally, turn 15 can be paired only with turn 17. So, for a spacing of 2, the count is only 2.

Next, we look at a spacing of 3. This time, turn 5 can be paired with turns 2 and 8, turn 7 can be paired with turns 4 and 10, and so on, so that for a spacing of 3, there are 10 occurrences. We can now see that when the spacing is an odd number, we don't have the situation of like coloured turns pairing up, and so the pair count is simply 2n_S. Good. We've found a pattern for odd numbered spacings.

Next, we look at a spacing of 4. In this case turn 5 can be paired only with turn 1, and turn 7 can be paired only with turn 3. Turns 9 and 11 cannot be paired at all. Turn 13 can be paired with turn 17, and turn 15 can be paired with turn 19. So, for a spacing of 4 we have 4 occurrences. It appears that we now also have a pattern for even numbered spacings: for a spacing of k, the number of occurrences is k. At least that's the pattern until one of several things happens. Regardless of whether the spacing is even or odd, the pair count can never be more than 2n_S. So, we can say that for an even numbered spacing k, the pair count is the lesser of k and 2n_S.

If the secondary winding were located in an infinitely long primary winding, the pattern which we've determined would be complete. However, we see that as the required spacing increases, we eventually run off the end of the coil. So, we have to account for that situation. When the spacing reaches 5, turn 5 loses one of it's pairings. When the spacing reaches 7, then both turns 5 and 7 lose one of their pairings. In general when the spacing value becomes greater than or equal to a, then the count must be reduced. In terms of a computer formula the reduction is:

However, for small values of k, this formula will give a negative number, and for large values of k, it will give an ever increasing value which, in fact, should never exceed n_S. Therefore we include Max() and Min() functions to limit the values to the correct range:

This now gives a proper correction when we run past the left end of the coil, but we also need one for the right end:

Now that we can precisely count each category of turn pairs, it's simply a matter of coding it into a variation of previously discussed mutual inductance summation functions:

The function shown above, is a straightforward implementation of the mutual inductance summation algorithm modified for the mystery coil. The formulae for the various turn pair counts are as described above. The variable k_even is used to keep track of even and odd values of k. It has a value of zero when k is odd, and a value of one when k is even. It was mentioned earlier that the brute force algorithm LpBrute() would come in handy later. Because of the rather complicated formula for counting the various pairs of turns in L_Mystery(), it's best to check it against a another method that's known to be correct. That's where the brute force algorithm comes in. It is slower because it must do many more calculations. However, the results of both algorithms are in complete agreement for many different test examples, and hence we can conclude there are no counting errors in L_Mystery().

The L_Mystery() function calculates primary self inductance L_P, secondary self inductance L_S, primary to secondary mutual inductance M_PS, total series aiding primary plus secondary self inductance L_T. However, because the BASIC function can only return a single value, the return statement must be modified to return whichever parameter is needed.

Following is a Javascript implementation of the same calculation:

It includes a Switch() construct to allow the user to select which of the calculated parameters is to be returned. The return parameter is determined by the value of the input variable sel:

This function has been expanded and implemented as an online calculator:

Javascript Mystery Coil Calculator.

Like other inductance calculators, this one lets us see the result of changing various dimensions and number of primary and secondary turns, as well as the effect on mutual inductance by changing the starting position of the secondary winding.

One thing that may be of interest is to see the effect of changing the relative start position of the secondary winding. The following diagrams show how the primary inductance varies depending on the relative position of the secondary winding:

The blue line is the inductance of the mystery coil primary, showing how it varies as the position of the secondary coil is shifted. The value a = 26 indicates the secondary is exactly centred, and this gives the minimum inductance in every case. The red line shows the inductance of an evenly spaced solenoid coil having the same length and same number of turns as the mystery coil primary. This is the inductance value that would be calculated by a traditional inductance formula using average pitch.

The next two diagrams show the same results for coils of different Diameter/Length ratios:

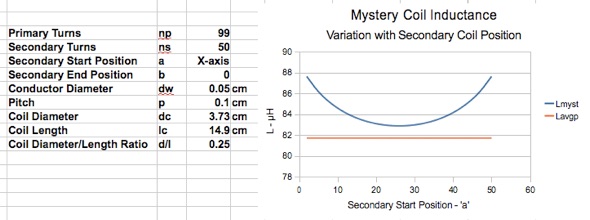
We see that, in all cases, the primary inductance is minimum when the secondary is centred relative to the primary. We also see that, as the coil's Diameter/Length ratio decreases, the mystery coil primary inductance increases, as compared to a winding of the same length with constant spacing.

It should be noted that, because of the vertical scale in the diagrams, the variation in inductance with secondary position is not as great as the curve may seem to indicate at first glance. However, this does give an indication of the amount of error that we may expect, if we use a traditional inductance formula to calculate the primary inductance based on averaging the turn spacing, instead of using the more accurate calculation.

Calculation of Inter-Winding Capacitance

As mentioned earlier, in the Mystery Crystal Set, there is no apparent signal path between the antenna and ground, and hence, the inter-winding capacitance is an important parameter. For that reason, it's useful to know the value of the inter-winding capacitance. This capacitance calculation is also included in the online calculator. It's based on the formula for the capacitance for two long parallel cylinders. In this case, the cylinders are the adjacent primary and secondary windings. The fact that these cylinders are wound around a coil form has very little effect on capacitance, as long as the wire diameter is considerably less than the coil diameter, which is generally the case. Complicating matters, the dielectric which separates the 'plates' of the capacitor consists of three different materials: the wire insulation, the coil form material, and air. The relative permittivity values, ε_R, (aka, dielectric constant) for these are typically as follows:

• Modern magnet wire enamel insulation: 3 to 3.5;
• Coil form materials: 2 to 3.5;
• Air: 1.

On this basis, the effective value of εR will be somewhere between 1 and 3.5. We can do the calculation with the low value and then repeat it with the high value to see the range of capacitance values.

Practical Example

In order to test the Online Calculator, I wound a mystery coil using an empty vitamin bottle as the coil form.

Coil specifications are as follows:

• Number of primary turns: 51;
• Number of secondary turns: 25;
• Secondary start position a: 15;
• Coil diameter: 76.76 mm;
• Total coil length: 42.85 mm;
• Coil form material: HDPE, ε_R = 2.3;
• Wire type: #24 AWG magnet wire, polyamide insulation: ε_R = 3.5;
• Estimated effective ε_R: 2;
• Conductor diameter: 0.5106 mm;
• Wire outside diameter including insulation: 0.5588 mm;
• Winding pitch: 0.5638 mm.

Aside from the modern materials, this is very close to the specifications for the coil in the original Mystery Set article.

The output from the calculator is:

Actual coil measurements:

Primary winding

Measurement Notes

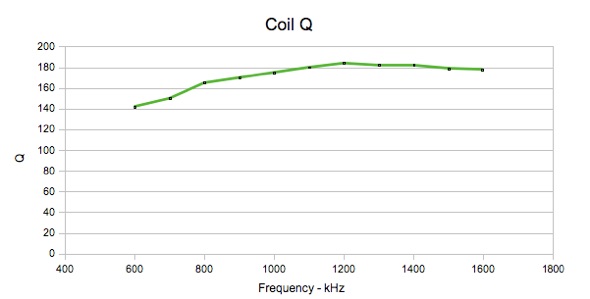
Inductance and Q measurements were done on an elderly but serviceable Heathkit QM-1 Q-meter by finding the parallel capacitance necessary to resonate with the coil at a number of different frequencies (exact frequency measured with an external HP 5381A frequency counter), and then performing a regression analysis to calculate both the winding inductance and self-capacitance C₀, which is also shown for each winding.

The primary self-inductance was measured over 11 different frequencies from 600 kHz to 1600 kHz. Standard deviation in the measured L and C₀ values are 2.65 µH and 1.4 pF respectively.

Secondary self-inductance was measured over 17 different frequencies from 1000 kHz to 3000 kHz. The Q values ranged from 95 at the highest frequency to 80 at the lowest frequency, and peaking at 96 at 2200 kHz. Standard deviation in the measured L and C₀ values are 0.18 µH and 1.3 pF respectively.

Secondary self-inductance was also measured with a simple L/C meter, but has no correction for C₀. Consequently, the reading is higher than that given by the Q-meter method.

Combined Primary plus Secondary inductance L_T+ was measured over 8 different frequencies from 240 kHz to 350 kHz. The Q values ranged from 11 at the highest frequency to 59 at the lowest frequency. Standard deviation in the measured L and C₀ values are 3.4 µH and 6.2 pF respectively.

Combined Primary minus Secondary inductance L_T– was measured over 6 different frequencies from 630 kHz to 800 kHz. The Q values ranged from 4 at the highest frequency to 11 at the lowest frequency. Standard deviation in the measured L and C₀ values are 0.63 µH and 14.8 pF respectively.

Combined Primary plus Secondary inductance L_T+, and Primary minus Secondary inductance L_T–, were also measured with Meter-1 and Meter-3, mentioned below. However, these measurements did not produce meaningful results, most likely because of the extremely large values of self-capacitance.

The calculated and measured parameters are summarized in the following table:

Allowing for experimental error, I would consider agreement to within 3% to be quite acceptable. Since the worst deviation here is only 1.34%, I believe this should validate the accuracy of the calculator.

Inter-Winding Capacitance Measurements

Inter-winding capacitance was measured with three different meters:

• Meter-1: Inexpensive L/C meter; measurement frequency: 8 kHz;
• Meter-2: Medium quality digital multimeter with a capacitance function; measurement frequency estimated to be ~10 kHz;
• Meter-3: Better quality L/C meter; measurement frequency: ~600 kHz.

If we take the inter-winding capacitance mean value of 1510 pF to be correct, then we can rerun the calculator with different values of ε_R in order to find which one gives the same value of 1510 pF, and thus get a better estimate of the true effective ε_R value. Doing this, we get a value of ε_R=2.04, which seems reasonable. However, we have to be careful in interpreting the results, because there is no guarantee that 1510 pF is the correct value. It's very likely that coil inductance has affected the capacitance measurement. This is a subject for future study. Regardless, the measured inter-winding capacitance values are in the same ballpark as the calculated value, and for something as non-critical as a Mystery Crystal Set, that's probably good enough.

In any event, the calculator can be run with the minimum and maximum values of ε_R to get capacitance values which will bracket the true value. For this example, these values of ε_R are 1 and 3.5 which give capacitance values of 741 pF and 2593 pF.

Coupling Coefficient

One other significant parameter in the mystery coil is the coupling coefficient  between primary and secondary. The calculated value of 0.8851 shows a high degree of coupling between primary and secondary, as we might expect with a bifilar close wound coil. However, it is even more interesting to look at the coupling between the secondary and just the adjacent portion of the primary. To do this, we change the number of primary turns n_P, to be n_S+1, or 26, and the secondary start position, a, to be 2. Doing this with the example coil, we get a coupling coefficient of 0.9871 which is close to the value of 0.966 determined by Ben Tongue in his analysis of the circuit. With such a high coupling coefficient, the coil behaves more like a transformer than a loosely coupled coil, and as Ben concluded, the secondary could very likely be omitted and replaced with taps on the primary at the 25 and 38 turn positions. Then, a physical capacitor could be added in the antenna lead, to account for the inter-winding capacitance. This would result in a simpler receiver, likely with the same performance.

Conclusion

Study of the Mystery Crystal Set coil has provided an opportunity to show how the mutual inductance summation method can be adapted to different special situations. This has also provided the opportunity to compare calculated values with actual measurements, and satisfy ourselves that the numbers provided by theoretical calculations do indeed agree quite well with reality.

Continue to: