Loop Antennas

In February 2008, I wanted to try my hand at building a tuned loop antenna suitable for the medium wave broadcast band. I decided to build a flat spiral loop for no particular reason other than the fact that I thought it would look nicer than a helical loop. I chose hexagonal over square for the same reason.

A tuned loop antenna consists of a loop of wire of one or more turns, connected in parallel with a variable capacitor. This forms a parallel resonant circuit which, if the component values are correctly chosen, can be tuned across the band of frequencies we are interested in. The tuned loop antenna may also include a second “pickup” loop which is connected to the antenna input of the radio receiver. This pickup loop acts as an impedance matching secondary winding to better transfer the signal to the receiver. If it is omitted, the receiver input is taken directly from the tuned winding, and other means may be required to impedance match to the receiver. I chose to use a pickup loop on my design.

The first step was to pick a convenient size for the loop. The larger the loop, the more signal it is capable of picking up. I chose a diameter of approximately 30 inches, since that seemed to be the largest size that I could conveniently build without it being overly cumbersome. For a description the construction go here.

The next step was to determine the required inductance, and from that, the required number of turns. I had a 480 pF variable capacitor, and using the LC resonance formula, came up with a required inductance value of 181 µH in order to tune down to 540 kHz. Knowing the required inductance, I needed to work out how many turns of wire would be required. Unfortunately, I wasn’t able to find any accurate inductance formulae, online, applicable to flat hexagonal loops, or even flat round spiral loops. I ended up using the closest formula I could find which was Wheeler’s spiral coil inductance formula. This formula is reasonably accurate when used within its limitations, but what I was doing went well beyond its limitations. However, it did give me a ballpark idea for the number of turns required. I was then able to experimentally adjust the number of turns until I got the inductance needed to resonate with the variable capacitor that I intended to use with it. Although the end result worked reasonably well, I noticed that the loop didn’t tune exactly as it should. I began to suspect that the self-capacitance of the loop was having a significant effect. This led to a bit of research which resulted in some tools to help better design, build and test a tuned loop antenna.

Here is a summary of my conclusions:

• A better formula for determining the inductance of loop antennas is needed.

• Cheap L/C meters do not measure the inductance accurately enough to be trusted.

• Self-capacitance in loop antennas will significantly affect the tuning of the loop, and so it must be accounted for.

To address the need for a better inductance formula, in the last couple of years, I've accumulated several more accurate inductance formulae. For polygonal spiral and helical antennas, I've created two spreadsheets which you can find on my Downloads Page. I've also created two online calculators which are accurate for circular and rectangular helical loops:

Circular Coil Inductance Calculator

Rectangular Coil Inductance Calculator

Regarding the LC meter, my particular L/C meter is quite accurate measuring capacitance, and the inductance of small coils. However, I discovered that large coils having a significant resistance, would have a measured inductance as much as 30% higher than the actual value. From this, I concluded that what I thought was a 180 µH loop was something much less. However, it was still tuning down to the bottom of the broadcast band, so there had to be something else at work too. This was where I suspected significant self-capacitance. This would have the effect of lowering the resonant frequency of the loop, because it would act in parallel with the variable capacitor.

I looked for another way to measure the inductance, as well as a method of measuring the self-capacitance. As it turns out, there is a measurement method which gives both the inductance and self-capacitance. It involves resonating the loop with several known capacitance values, noting the resonant frequency and the capacitance for each different measurement, and then performing a least squares analysis. This is much easier than it sounds. It can be done with a simple spreadsheet. The minimum required number of frequency/capacitance measurements that must be made, is two. However, accuracy (and confidence) improves with more measurements. As well, using more measurements will also provide information about how constant the self-capacitance and inductance values are across the frequency band of interest. If the measurements are done carefully, then all of the points will lie on a straight line, and it’s then possible to use lumped component values for the inductance and self-capacitance.

Using the LC resonance formula:

F=1/(2π √(L x (Cv+Co)))

where:

F = resonant frequency

L = loop inductance

Cv = External variable capacitance

Co = Loop self-capacitance

The formula can be rearranged to get Co in terms of the other variables:

Co = 1/(4π2 x F2 x L) - Cv

Now, if we do tests at several different frequencies, adjusting Cv to resonate the circuit at each of these frequencies, we can use these values of Cv to calculate the value of Co at each of these frequencies.

There are several ways to set up the test equipment to do the measurements. In my case, I connected a diode detector to the antenna’s pickup loop and monitored the signal on a pair of sensitive high impedance headphones. The signal source was a loop of several turns of wire connected to an RF signal generator, and located a couple of feet from the loop antenna. The results of the tests at eight different frequencies are shown in the spreadsheet below:

The first column is the test frequency. The second column, Cv, is the measured value of external capacitance required to resonate the circuit. Cell C4 is the loop inductance estimate (actually measured by the LC meter with dubious accuracy). Column D calculates the total net circuit capacitance required to resonate with the loop inductance at the indicated frequency. This is calculated from the resonance formula rearranged thus:

C_eff = 1/(4π2 x F2 x L)

From the above discussion we know that the net capacitance is equal to the value of Cv plus the loop self-capacitance Co. However, the measured value of Cv includes additional capacitance (13 pF in this case) due to the test leads of the LC meter. Subtracting the test lead capacitance gives the corrected value of Cv’ in column E. And finally as discussed above, the value of Co is given in column F by the formula:

Co = C_eff - Cv’

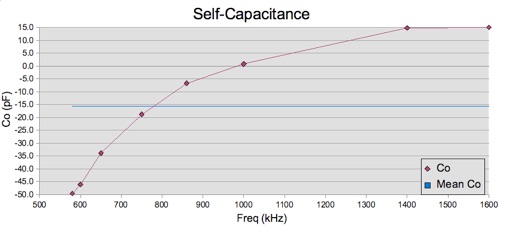
Notice that this value varies from 15 pF down to –50 pF, not the constant value that we were expecting.

If we were to plot the results of the test on a graph, we had hoped to draw a straight horizontal line through all of the points. However, using the data that was obtained from the test, we get the following instead:

Referring back to the spreadsheet, at the bottom of column F is the calculated mean value of the eight Co values. Column G contains the square of the difference between each Co value and the mean Co value. Cell G13 contains the sum of the square of the differences ∑e². We will use this value (the lower the better) as a measure of the goodness of fit of the data to our goal of a constant Co value.

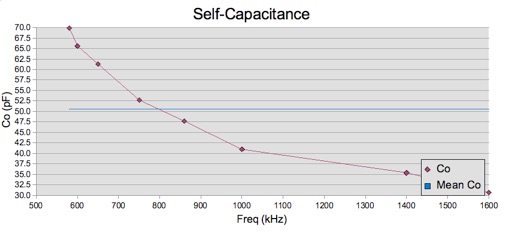
Where do we go from here? As I mentioned earlier, the measured inductance value was suspect. So, let’s adjust the estimated value down from 180 µH to 160 µH and recalculate Co from the same experimental data. We now get the following graph of Co:

This is an improvement. The values are now all positive and lie over a narrower range: 2.5 pF to 23 pF. So let’s reduce our estimate of L down to 140 µH and try again. This time we get:

We have gone too far, and now the curve bends the other way. So we can assume that the true value of L is between 140 and 160 µH. Rather than repeatedly trying different values for L, we can use the goal seek function of the spreadsheet to adjust the value of L until it finds the minimum value for ∑e² (the sum of the squares of the errors). This gives us the value of L=152.09 µH, and a ∑e² value of 8.1 as shown in the revised spreadsheet.

This is considerably better than the original ∑e² value of 4641 from the first calculation. As well, the values of Co now lie in the narrow range of 25 to 28 pF. These results are shown in the following graph:

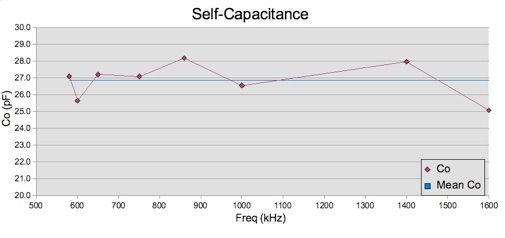
The values now lie along a straight horizontal line, with  a mean value for Co = 26.9 pF. The expanded scale of this graph accentuates the measurement error, but since the points randomly fall on either side of the mean value, it appears that we have reached the best fit within the limits of experimental error.

The importance of making multiple measurements should now become clear. If we had only made measurements at two frequencies, we could still have done a least squares fit (or a direct analytical calculation) to produce a single L value and a single Co value, but we wouldn’t have any confidence that the data wouldn’t bend up or down between those points due to some other unknown influence. This graph shows that given an L value of 152 µH we can be certain of a constant Co value over the frequency range of interest. These values can then be used to determine other circuit component values.

Although the above manual manipulation of the numbers is interesting, in that it shows how the curves bend up or down when the estimated values for Co are varied, there is a more direct least squares calculation method using a method developed by Whittemore and Breit (Physical Review, Vol. XIV, No. 2, page 170). I’ve created a spreadsheet that performs this calculation. It is available as an OpenOffice/LibreOffice ods file, and an Excel xls file. It is simply a matter of entering the tuning capacitor values and the resulting resonant frequencies.

Using the polygonal spiral inductance spreadsheet mentioned earlier, the calculated inductance value of my loop antenna is 152.8 µH, an agreement within a half percent of the value determined from the least squares analysis. While I haven’t tested this formula on any other loops, the fact that it was so close to the measured value for this one example, makes me confident enough to recommend its general use.