Mini-Tube Audio Amplifier - Part 1

It would appear that there comes a time for every electronics experimenter where they feel the need to build a tube audio amplifier. And so it has come to pass with me. For my first serious attempt, I decided to keep things rather conservative—under 1 kilowatt. Well actually, under one watt per channel.

Warning: This is not intended as a step by step DIY construction project. It's a discussion of my experience building this project, and an explanation of the various design, construction and testing stages. I recognize that some people may use this information to build their own version of this project. Consequently, take notice that there are high voltages present in this circuit which can be lethal. These voltages are significantly higher than those of other tube electronics projects which appear on this web site. Proceed at your own risk.

A discussion came up on one of the news groups some time ago about building the smallest (or simplest) push-pull tube audio amplifier. This got me thinking about making a one tube push pull amplifier (two tubes for stereo). I had a few 6M11 Compactron tubes on hand that I previously used to build this AM transmitter. These tubes have a pentode section plus two identical triode sections. I thought that the pentode would be a good preamp, while the triodes would serve as the push-pull output. The triodes are only rated for a maximum plate dissipation of 2.25 watts each. So, this is definitely a low power audio project (less than a watt RMS per channel). But, it seemed like a good application to drive desktop speakers from a computer audio output. Just to keep things in perspective, here is a picture comparing the size of a 6M11 with the well known 6SN7GT. As you can see, this is a rather tiny tube, considering that it comprises three sections.

Using the pentode section as a preamp, and the triodes as the output stage, there's no section left to act as a phase inverter. There are other options however. Some of the earliest designs fed the push-pull output stage from a centre tapped inter-stage transformer which accomplished the phase inversion task. However, I decided that inter-stage transformers are a rather dated design technique. Instead, I decided to drive one half of the push-pull output directly from the pentode preamp stage, and then use the plate signal from the first triode to drive the second triode. To do this, the triodes must not be cut off for any part of the input cycle. In other words, they must operate in Class A mode. This isn't a big deal, because the reduced efficiency of Class A mode makes little difference at these low power levels.

This is the prototype circuit:

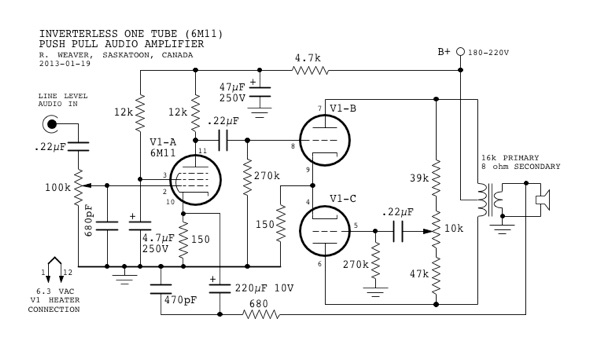
Click for a larger View

And here is the original breadboard assembly:

The output transformer has its primary taps wired to a 2 pole multi-position rotary switch in order to test different impedance ratios on the fly.

The Preamp Stage

The preamp stage is a standard cathode biased amplifier stage. The cathode resistor is not bypassed, because this stage already has sufficient gain, and by leaving the cathode resistor unbypassed, it provides a means to introduce negative feedback later. The voltage gain is approximately equal to the plate load resistor divided by the cathode resistance, or:

Av = 12000 / 150 = 80

Note the 680 pF shunt capacitor at the input. I added this after discovering that many digital audio sources have insufficient filtering, and include sampling frequency noise components at around 44 kHz. I didn't want this passing through the amplifier. This low value capacitor removes the high frequency noise without affecting audio frequency signals.

The Push-Pull Output Stage

I mentioned that the inverted input to the second output triode would be taken from the plate of the the first triode. In fact, this is only partially true. Because the two triode sections share a common unbypassed cathode resistor, the output stage acts as a cathode coupled differential amplifier. However, because of the relatively low value of cathode resistor, the cathode current will not be constant as it would in a normal differential amplifier (rather than the traditional 'long-tailed pair', we have, so to speak, a 'short-tailed pair'). Therefore, the cathode drive to the second triode will not produce an equal plate swing. In a normal cathode coupled stage, the grid of the second triode would be grounded. However, in this circuit, the grid of the second triode receives a small amount of signal from the plate of the first triode to compensate for the insufficient cathode drive.

The potentiometer in the voltage divider shown on the right side of the diagram is adjusted to get the proper level of inverted signal to drive the grid of V1-C. One interesting thing to note, is that this voltage divider must connect to the opposite ends of the output transformer, rather than from V1-B plate to ground. This is because, in the latter case, there would be a positive feedback effect which makes the stage unstable. This happens because, as the plate of V1-B goes more negative, causing the grid of V1-C to go more negative, the plate of V1-C then goes more positive, and because of the coupling between V1-B and V1-C plates due to the autotransformer effect of the output transformer primary, this causes the plate of V1-B to go even more negative. Hence, the positive feedback situation, and adjustment of the V1-C drive potentiometer is very touchy. By connecting the lower leg of the drive potentiometer to the V1-C plate, this introduces a slight negative feedback to counter the positive feedback. Adjustment of the drive pot, is then much smoother.

Up to this point, circuit component values and power supply voltage were selected based on a preliminary load line analysis using a slightly modified single ended loadline. This was fine for determining quiescent operating plate voltage and current and grid bias, but not ideal for determining plate dissipation, output impedance matching or power output. For that, composite plate curves are needed. However, they are laborious to produce manually, and must be completely redone whenever the operating point changes.

During this time, I had been doing some research on vacuum tube SPICE models. It appeared to me that at the present time the most accurate triode model is the one given on Norman Koren's Site. His plate current formula is:

I_P = (E₁^X/k_G1)(1 + sgn(E₁))

where the value E₁ is given by:

E₁ = (E_P /k_P) log(1 + exp(k_P(1/µ + E_G /sqrt(k_VB + E_P²))))

where E_P is plate voltage, E_G is grid voltage, and the remaining variables k_P, µ, x, k_G1 and k_VB are constants which depend on the tube characteristics. The sgn() function returns +1 if the argument is greater than zero, and −1 if the argument is less than zero. By tabulating the data from the published 6M11 triode plate curves, entering them into a spreadsheet, and then performing a multi-variable optimization, I was able to determine the values of the constants to be:

µ = 84.8

x = 0.98

k_G1 = 162.87

k_P = 243.8

k_VB = 2664.39

Using these values, Koren's triode formula models the published triode plate curves very precisely. In fact, manufacturing variations between tubes would create deviations greater than those of the model. Rather than model the circuit in SPICE, I chose to use the spreadsheet to create the tube curves and load lines. In creating the load line, I used the original circuit component values, and then refined them during the analysis. A graph based on adjusted component values is shown below:

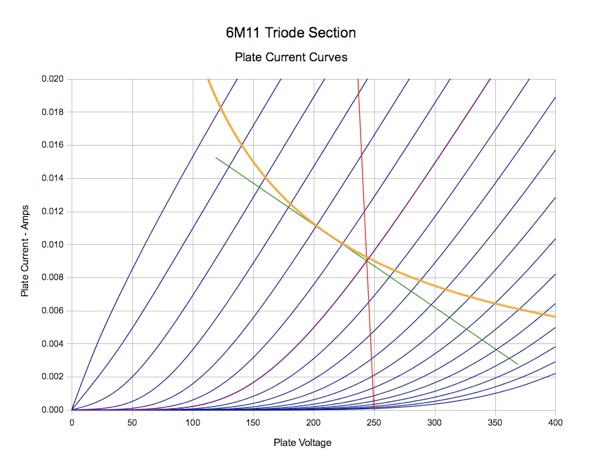
The blue lines are Plate Current vs. Plate Voltage for grid voltage increments of 0.5 volts for each curve. Normally, the first curve on the left is 0 grid volts, and then each curve increases in round numbers. However, this graph has the grid voltages shifted slightly so that one of the curves (violet) will pass exactly through the quiescent operating point. In this case, it corresponds to a grid bias of −2.84 volts. The curves moving away from the violet one change by increments 0.5 volts, in order to preserve linear display of the I-V characteristics.

The red line is the static load line, and the green line is the dynamic load line.

The orange line is the locus of maximum allowable plate dissipation which is 2.25 watts for the 6M11 triode section. To stay within the tube's allowable ratings, the quiescent point must be below this line, and ideally the entire dynamic load line should remain under the this line as well. However, as long as most of the dynamic load line remains below the maximum dissipation line, the average power will generally be less than the maximum, and this is acceptable. That didn't appear to be a problem in this situation, because the dynamic load line just touches the maximum dissipation line at one point and otherwise remains in the safe area. It can be seen immediately that the original plate supply of 180-220 volts has been increased to 250 volts. The static load line includes a cathode bias resistance of 160 ohms plus transformer primary winding resistance of 350 ohms. When creating the load line for one tube, because the cathode resistor will be shared by two tubes, its value must be doubled. Hence the total DC load resistance will be 160x2+350=670 ohms.

From the analysis, the quiescent operating point gives a plate voltage of 244 volts, plate current of 9 mA, and a quiescent plate dissipation of 2.2 watts. As mentioned previously the grid bias is −2.84 volts.

It became apparent that the dynamic load of 16k was a bit too low, and so it was changed to 20k. Fortunately, I had another output transformer available with a 20k primary.

An advantage of having an accurate plate current formula in the spreadsheet is that composite push-pull plate current curves can be generated.

Following is the set of composite characteristic curves:

Again, the central violet curve corresponds to the chosen grid bias of −2.84 volts. Each curve moving away from the central one has an incremental grid voltage of ±0.5 volts.

Note how the combined plate curves show amazingly good linearity, both in the even spacing between curves (indicating constant gain over over the full dynamic range), as well as constant slope of the curves (indicating a constant output impedance over the full dynamic range). It should be mentioned that the first two and last two curves have positive grid voltage (+0.16V and +0.66V) on one of the triodes. My past experience shows that these triodes draw very little grid current when positively biased, and it can be seen here that as long as the tube model is still accurate in this region, then linearity continues to be very good.

Maximum power output is achieved when the slope of the dynamic load line (green) is the reverse of the slope of plate curves. It can be seen that this is the case, with the chosen load impedance of 20k.

Maximum Plate Dissipation Curves

Whereas generating the composite plate current curves was relatively painless, calculating the maximum plate dissipation locus turned out to be quite a challenge. It's easy to do on the single ended curves, as one simply plots the line I=P_Max/V. However, on the composite curve graph, the current axis is differential current and there is no direct way to determine the maximum differential current given a plate voltage value. The solution involves tracing along each composite curve to find the point where I × V for a single tube is equal to P_Max, and then recording that point. This is repeated for each curve, and then a line is drawn through all of these points to produce the maximum plate dissipation curves. Doing this on a spreadsheet requires a lot of calculation cells and is a bit messy, but it can be done. The result of all this is the following composite curves which include the maximum plate dissipation lines (in orange). The upper line indicates the upper limit for the upper tube, and the lower line indicates the lower limit for the bottom tube. The safe operating range is the band between the orange lines. To avoid exceeding maximum plate dissipation ratings, the dynamic load line should be between these two limits.

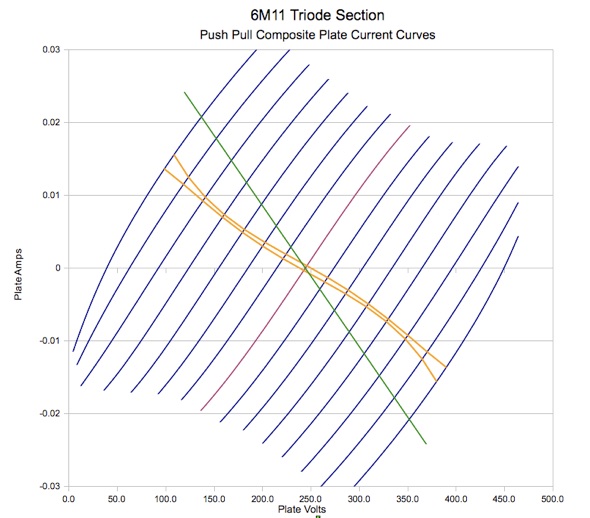
Not good! Obviously, I did a poor job picking the operating point. The good thing is that the composite curves immediately reveal the problem. At this point I decided to reduce both plate voltage and plate current, and try again. The advantage of having everything on a spreadsheet is that the results of any change are immediately displayed. Here is the next attempt using a plate voltage of 240 volts and plate current of 7 mA:

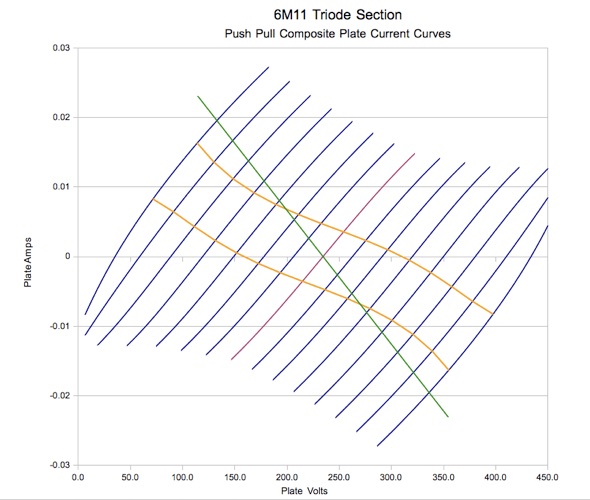
This is better, but at high output levels the maximum allowable plate dissipation of each triode will still be exceeded part of the time. By increasing the load impedance to 30,000 ohms, the dynamic load line can be made to fit within the allowable power band as shown in the next graph below:

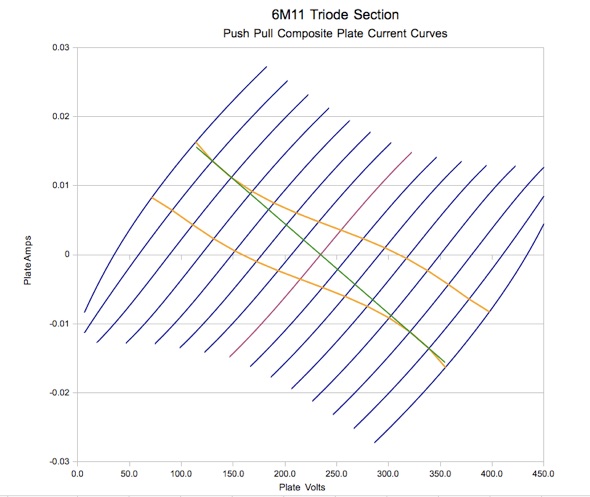
This shows a voltage swing of 240 volts peak-peak into the 30k load which gives an output power of 0.24 watts RMS, which is less than I'd been hoping for. In the end, partly because I didn't have a 30k output transformer, I opted for the design shown in the previous chart which gives 0.36 watts, and stays within the maximum dissipation ratings on average.

Having nailed down the basics of the amplifier, I decided to add some refinements. These are discussed in the next few sections.

Negative Feedback

From initial testing, the amplifier has a reasonable frequency response (considering the inexpensive output transformer) of 25 Hz to 15 kHz, and reasonably low distortion. However, the amplifier has plenty of gain, and it makes sense to take advantage of the excess gain, and introduce some negative feedback to improve frequency response and further reduce distortion. There are several ways to incorporate negative feedback. The method I chose was to take the output signal from the output transformer secondary back to the cathode of the pentode section.

Adding negative feedback to a high gain amplifier introduces the risk of instability, and the possibility of the amplifier breaking into oscillation. This happens because certain reactive circuit components cause phase shift, and at certain frequencies the combined phase shift can reach 180°, at which point the amplifier becomes an oscillator. Most of the phase shift comes from the output transformer, generally at high audio or ultrasonic frequencies. There are a couple of methods to prevent this from happening. The first is to add a parallel RC network, in the feedback path, which has a complementary phase shift characteristic thus reversing the phase shift introduced by the output transformer. The second method is to add an RC low pass filter, in the feedback path, which rolls off the feedback to a sufficiently low level at higher frequencies so that at the point where the net phase shift reaches 180°, the total loop gain is less than one, and oscillation is not possible. This second method is the approach that I used. The 470 pF capacitor in combination with the feedback resistor (680 ohms in the above schematic diagram) accomplishes the feedback roll-off.

With negative feedback applied, the 3db frequency response is now 20Hz to 70 kHz.

Tone Control

I decided that the amplifier needed a tone control. I wanted something better than a simple adjustable RC low pass filter, but at the same time, wanted to stay with a single knob control. It must be a passive circuit, since I've already used up all the tube sections, and the tone control must be outside of the negative feedback loop. This means that it has to be right at the input, or else at the speaker. (Tone control at the speaker has been done, but requires some odd component values.)

After a bit of web searching, I found two particularly interesting tone control circuits:

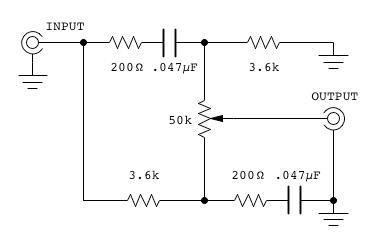
Derek Bowers simple tone control article in EDN (Electonic Design News)

His circuit is shown below:

Frequency Response of the Bowers' tone control:

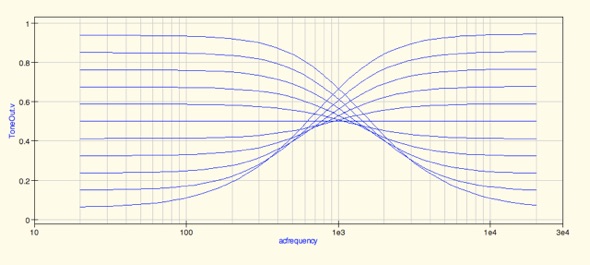
The Bowers circuit looks very good. Bass boost and treble cut at one end of rotation, and then treble boost and bass cut at the other end; completely flat at mid-rotation, and very significant amounts of boost and cut at the end positions. In addition, the circuit is very simple.

The only problem is that it requires a very low impedance signal source (<200 ohms), and a very high load impedance. The high load impedance is normally not a problem with a tube, but I still need a volume control, and that means something in the 500k range in order not to load down the tone control output. Using high resistance volume controls can lead to increased hum and noise though. I also found that some of my audio input sources have significantly higher impedance than 200 ohms, which would therefore require an additional buffer stage prior to the tone control.

I didn't immediately rule out the Bowers' tone control, but decided to look at some tone controls that were specifically intended for tube amplifiers.

The next one that I looked at is Simcha Delft's 'Moonlight' tone control.

The circuit is shown below:

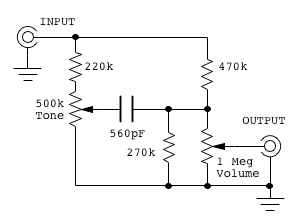
This one is intended for a tube amp, and has component values more in line with what I was looking for. It also allows for (and includes) the volume control. The 1 Megohm volume control resistance is higher than desirable, but the 270k fixed resistor and 1 Meg. pot can be replaced with a 250k pot. Additionally, all of the component values can be scaled down to more acceptable ones without affecting frequency response.

Unlike the Bowers circuit, this circuit only gives treble boost/cut, and leaves the bass unaffected.

Frequency Response of Simcha Delft's 'Moonlight' tone control:

That may not be such a big deal since everything is relative, but the treble boost/cut is about half the range that the Bowers circuit gives. So relatively speaking the overall effect is the about 1/4 of the former circuit. Furthermore, since this circuit doesn't give a complementary bass cut/boost, the tone control affects the perceived overall volume.

Since I'd been running simulations of both of these circuits anyway, I decided to experiment with different configurations. I eventually came up with another bridge circuit, somewhat different from Delft's:

My bridge tone control:

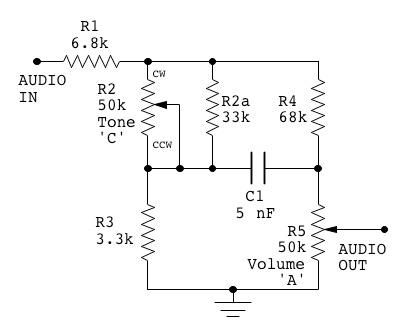
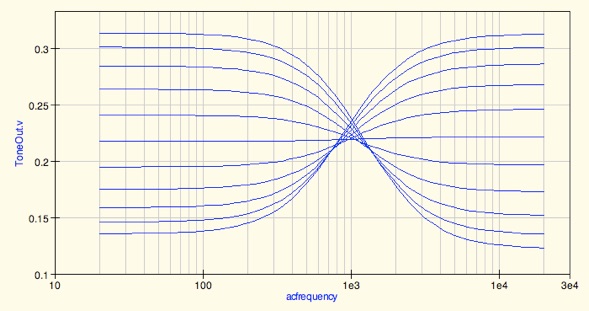
Interestingly, by adding the input resistor, changing the tone potentiometer to a two wire variable resistor configuration, and changing other component values, the circuit gives bass boost and treble cut at one end of rotation, and bass cut and treble boost at the other end of rotation. Though the total amount of boost/cut is equal for bass and treble, using a linear taper control, it can be seen from the following frequency response graph that the control adjustment characteristic is not linear.

Each curve on the graph is an equal increment of tone control resistance. The control characteristic falls roughly halfway between linear taper and reverse audio taper. However, by paralleling a fixed resistance with an audio taper control, the control action becomes much more linear, and gives flat response at mid position, as shown in the next graph where each curve is an equal increment of control rotation:

The final tone control circuit is shown below:

As previously mentioned, for a proper linear control characteristic, the tone control must be a reverse audio taper (also known as C-taper) or else a standard audio taper control must be wired so that bass increases with clockwise rotation, and treble increases with counter-clockwise rotation. I decided to use a standard audio taper control, and live with the reverse operation (and redesignate it as a bass control). If the constructor is not concerned about having the flat response exactly at mid rotation, then a 20k or 25k linear taper control (in place of the 50k pot & 33k fixed resistor) gives perfectly acceptable performance. My personal preference was to have flat response at mid-rotation (making it easier to do frequency response testing among other things), so I went with the audio taper arrangement.

This tone control is not as fussy about input signal impedance as long as it doesn't begin to approach the value of R₁. Also, the tone control and volume control are identical in value which helps in sourcing parts.

There are always compromises though. The boost/cut ratio is slightly higher than Delft's circuit, but still only about a third of the Bowers circuit.

Here is a summary of the tone control characteristics:

• Frequency response is flat when R₂/R₃ = R₄/R₅ (ie., the bridge is balanced, hence no current passes through the capacitor which is the only reactance in the circuit). With the component values given, R₂ (actually, the net value of R₂ in parallel with R_2a) is adjusted to 4.5k for flat response. That works out to be mid-position for an audio taper pot.

• For equal boost and cut range, the R₂ value should be about 8 times the R₃ value.

• For equal treble and bass adjustment range, R₁ should be equal to R₂+R₃ (when R₂||R_2a is set to flat position: 4.5k). To be more precise, R₁ should be equal to the combined resistance of the parallel combination of (R₂+R₃)||(R₄+R₅), but since R₄+R₅ is much greater than R₂+R₃, it doesn't affect the value significantly.

• Doubling R₁ makes the bass boost/cut range double the treble boost/cut range.

• Likewise, halving R₁, halves bass boost/cut range relative to treble range.

• For the resistance values shown, the C₁ value is determined from the desired crossover frequency, F_C, according to: C₁=0.005/F_C, where capacitance is in microfarads, and frequency is in kilohertz. So, a 0.005 µF capacitor gives a crossover frequency of 1 kHz.

Though 1 kHz crossover frequency seems to be standard in most of the tone controls I've seen, I find this a bit high for my taste, and I opted for a lower frequency using a capacitance of 0.0068 µF resulting in a crossover frequency of 735 Hz.

One rather useful thing about this circuit (as with Delft's) is that since the crossover frequency is set by a single capacitor, different values can be switched in, to change F_C.

Continue to Part 2